Lifelong Learning

March 6, 2022

Lifelong learning–especially if pursued in a multidisciplinary fashion–can continuously improve your productivity and ability to think. Lifelong learning boosts your capacity to serve others.

Robert Hagstrom’s wonderful book,Investing: The Last Liberal Art(Columbia University Press, 2013), is based on the notion of lifelong, multidisciplinary learning.

Ben Franklin was a strong advocate for this broad-based approach to education. Charlie Munger–Warren Buffett’s business partner–wholeheartedly agrees with Franklin. Hagstrom quotes Munger:

Worldly wisdom is mostly very, very simple. There are a relatively small number of disciplines and a relatively small number of truly big ideas. And it’s a lot of fun to figure out. Even better, the fun never stops…

What I am urging on you is not that hard to do. And the rewards are awesome… It’ll help you in business. It’ll help you in law. It’ll help you in life. And it’ll help you in love… It makes you better able to serve others, it makes you better able to serve yourself, and it makes life more fun.

Hagstrom’s book is necessarily abbreviated. This blog post even more so. Nonetheless, I’ve tried to capture many of the chief lessons put forth by Hagstrom.

Here’s the outline:

• A Latticework of Mental Models
• Physics
• Biology
• Sociology
• Psychology
• Philosophy
• Literature
• Mathematics
• Decision Making

(Image: Unfolding of the Mind, by Agsandrew)

 

A LATTICEWORK OF MENTAL MODELS

Charlie Munger has long maintained that in order to be able to solve a broad array of problems in life, you must have a latticework of mental models. This means you have to master the central models from various areas–physics, biology, social studies, psychology, philosophy, literature, and mathematics.

As you assimilate the chief mental models, those models will strengthen and support one another, notes Hagstrom. So when you make a decision–whether in investing or in any other area–that decision is more likely to be correct if multiple mental models have led you to the same conclusion.

Ultimately, a dedication to lifelong, multidiscipinary learning will make us better people–better leaders, citizens, parents, spouses, and friends.

In the summer of 1749, Ben Franklin put forward a proposal for the education of youth. The Philadelphia Academy–later called the University of Pennsylvania–would stress both classical (“ornamental”) and practical education. Hagstrom quotes Franklin:

As to their studies, it would be well if they could be taught everything that is useful and everything that is ornamental. But art is long and their time is short. It is therefore proposed that they learn those things that are likely to be most useful and most ornamental, regard being had to the several professions for which they are intended.

Franklin held that gaining the ability to think well required the study of philosophy, logic, mathematics, religion, government, law, chemistry, biology, health, agriculture, physics, and foreign languages. Moreover, says Hagstrom, Franklin viewed the opportunity to study so many subjects as a wonderful gift rather than a burden.

(Painting by Mason Chamberlin (1762) – Philadelphia Museum of Art, via Wikimedia Commons)

Franklin himself was devoted to lifelong, multidisciplinary learning. He remained open-minded and intellectually curious throughout his life.

Hagstrom also observes that innovation often depends on multidisciplinary thinking:

Innovative thinking, which is our goal, most often occurs when two or more mental models act in combination.

 

PHYSICS

Hagstrom remarks that the law of supply and demand in economics is based on the notion of equilibrium, a fundamental concept in physics.

(Research scientist writing physics diagrams and formulas, by Shawn Hempel)

Many historians consider Sir Isaac Newton to be the greatest scientific mind of all time, points out Hagstrom. When he arrived at Trinity College at Cambridge, Newton had no mathematical training. But the scientific revolution had already begun. Newton was influenced by the ideas of Johannes Kepler, Galileo Galilei, and René Descartes. Hagstrom:

The lesson Newton took from Kepler is one that has been repeated many times throughout history: Our ability to answer even the most fundamental aspects of human existence depends largely on measuring instruments available at the time and the ability of scientists to apply rigorous mathematical reasoning to the data.

Galileo invented the telescope, which then proved that the heliocentric model proposed by Nicolaus Copernicus was correct, rather than the geocentric model–first proposed by Aristotle and later developed by Ptolemy. Moreover, Galileo developed the mathematical laws that describe and predict falling objects.

Hagstrom then explains the influence of Descartes:

Descartes promoted a mechanical view of the world. He argued that the only way to understand how something works is to build a mechanical model of it, even if that model is constructed only in our imagination. According to Descartes, the human body, a falling rock, a growing tree, or a stormy night all suggested that mechanical laws were at work. This mechanical view provided a powerful research program for seventeenth century scientists. It suggested that no matter how complex or difficult the observation, it was possible to discover the underlying mechanical laws to explain the phenomenon.

In 1665, due to the Plague, Cambridge was shut down. Newton was forced to retreat to the family farm. Hagstrom writes that, in quiet and solitude, Newton’s genius emerged:

His first major discovery was the invention of fluxions or what we now call calculus. Next he developed the theory of optics. Previously it was believed that color was a mixture of light and darkness. But in a series of experiments using a prism in a darkened room, Newton discovered that light was made up of a combination of the colors of the spectrum. The highlight of that year, however, was Newton’s discovery of the universal law of gravitation.

(Copy of painting by Sir Godfrey Kneller (1689), via Wikimedia Commons)

Newton’s three laws of motion unified Kepler’s planetary laws with Galileo’s laws of falling bodies. It took time for Newton to state his laws with mathematical precision. He waited twenty years before finally publishingPrincipia Mathematica.

Newton’s three laws were central to a shift in worldview on the part of scientists. The evolving scientific view held that the future could be predicted based on present data if scientists could discover the mathematical, mechanical laws underlying the data.

Prior to the scientific worldview, a mystery was often described as an unknowable characteristic of an “ultimate entity,” whether an “unmoved mover” or a deity. Under the scientific worldview, a mystery is a chance to discover fundamental scientific laws. The incredible progress of physics–which now includes quantum mechanics, relativity, and the Big Bang–has depended in part on the belief by scientists that reality is comprehensible. Albert Einstein:

The most incomprehensible thing about the universe is that it is comprehensible.

Physics was–and is–so successful in explaining and predicting a wide range of phenomena that, not surprisingly, scientists from other fields have often wondered whether precise mathematical laws or ideas can be discovered to predict other types of phenomena. Hagstrom:

In the nineteenth century, for instance, certain scholars wondered whether it was possible to apply the Newtonian vision to the affairs of men. Adolphe Quetelet, a Belgian mathematician known for applying probability theory to social phenomena, introduced the idea of “social physics.” Auguste Comte developed a science for explaining social organizations and for guiding social planning, a science he calledsociology. Economists, too, have turned their attention to the Newtonian paradigm and the laws of physics.

After Newton, scholars from many fields focused their attention on systems that demonstrate equilibrium (whether static or dynamic), believing that it is nature’s ultimate goal. If any deviations in the forces occurred, it was assumed that the deviations were small and temporary–and the system would always revert back to equilibrium.

Hagstrom explains how the British economist Alfred Marshall adopted the concept of equilibrium in order to explain the law of supply and demand. Hagstrom quotes Marshall:

When demand and supply are in stable equilibrium, if any accident should move the scale of production from its equilibrium position, there will instantly be brought into play forces tending to push it back to that position; just as a stone hanging from a string is displaced from its equilibrium position, the force of gravity will at once tend to bring it back to its equilibrium position. The movements of the scale of production about its position of equilibrium will be of a somewhat similar kind.

(Alfred Marshall, via Wikimedia Commons)

Marshall’sPrinciples of Economics was the standard textbook until Paul Samuelson publishedEconomics in 1948, says Hagstrom. But the concept of equilibrium remained. Firms seeking to maximize profits translate the preferences of households into products. The logical structure of the exchange is a general equilibrium system, according to Samuelson.

Samuelson’s view of the stock market was influenced by the works of Louis Bachelier, Maurice Kendall, and Alfred Cowles, notes Hagstrom.

In 1932, Cowles founded the Cowles Commission for Research and Economics. Later on, Cowles studied 6,904 predictions of the stock market from 1929 to 1944. Cowles learned that no one had demonstrated any ability to predict the stock market.

Kendall, a professor of statistics at the London School of Economics, studied the histories of various individual stock prices going back fifty years. Kendall was unable to find any patterns that would allow accurate predictions of future stock prices.

Samuelson thought that stock prices jump around because of uncertainty about how the businesses in question will perform in the future. The intrinsic value of a given stock is determined by the future cash flow the business will produce. But that future cash flow is unknown.

Bachelier’s work showed that the mathematical expectation of a speculator is zero, meaning that the current stock price is in equilibrium based on an equal number of buyers and sellers.

Samuelson, building on Bachelier’s work, invented the rational expectations hypothesis. From the assumption that market participants are rational, it followed that the current stock price is the best collective guess of the intrinsic value of the business–based on estimated future cash flows.

Eugene Fama later extended Samuelson’s view into what came to be called the Efficient Markets Hypothesis (EMH). Stock prices fully reflect all available information, therefore it’s not possible–except by luck–for any individual investor to beat the market over the long term.

Many scientists have questioned the EMH. The stock market sometimes does not seem rational. People often behave irrationally.

In science, however, it’s not enough to show that the existing theory has obvious flaws. In order to supplant existing scientific theory, scientists must come up with a better theory–one that better predicts the phenomena in question.Rationalist economics, including EMH, is still the best approximation for a wide range of phenomena.

Some scientists are working with the idea of acomplex adaptive system as a possible replacement for more traditional ideas of the stock market. Hagstrom:

Every complex adaptive system is actually a network of many individual agents all acting in parallel and interacting with one another. The critical variable that makes a system both complex and adaptive is the idea that agents (neurons, ants, or investors) in the system accumulate experience by interacting with other agents and then change themselves to adapt to a changing environment. No thoughtful person, looking at the present stock market, can fail to conclude that it shows all the traits of a complex adaptive system. And this takes us to the crux of the matter. If a complex adaptive system is, by definition,continuously adapting, it is impossible for any such system, including the stock market, ever to reach a state of perfect equilibrium.

It’s much more widely accepted today that people often do behave irrationally. But Fama argues that an efficient market does not require perfect rationality or information.

Hagstrom concludes that, while the market is mostly efficient, rationalist economics is not the full answer. There’s much more to the story, although it will take time to work out the details.

 

BIOLOGY

(Photo by Ben Schonewille)

Robert Darwin, a respected physician, enrolled his son Charles at the University of Edinburgh. Robert wanted his son to study medicine. But Charles had no interest. Instead, he spent his time studying geology and collecting insects and specimens.

Robert realized his son wouldn’t become a doctor, so he sent Charles to Cambridge to study divinity. Although Charles got a bachelor’s degree in theology, he formed some important connections with scientists, says Hagstrom:

The Reverend John Stevens Henslow, professor of botany, permitted the enthusiastic amateur to sit in on his lectures and to accompany him on his daily walks to study plant life. Darwin spent so many hours in the professor’s company that he was known around the university as “the man who walks with Henslow.”

Later, Professor Henslow recommended Darwin for the position of naturalist on a naval expedition. Darwin’s father objected, but Darwin’s uncle, Josiah Wedgewood II, intervened. When the HMSBeagle set sail on December 27, 1831, from Plymouth, England, Charles Darwin was aboard.

Darwin’s most important observations happened at the Galapagos Islands, near the equator, six hundred miles west of Ecuador. Hagstrom:

Darwin, the amateur geologist, knew that the Galapagos were classified as oceanic islands, meaning they had arisen from the sea by volcanic action with no life forms aboard. Nature creates these islands and then waits to see what shows up. An oceanic island eventually becomes inhabited but only by forms that can reach it by wings (birds) or wind (spores and seeds)…

Darwin was particularly fascinated by the presence of thirteen types of finches. He first assumed these Galapagos finches, today called Darwin’s finches, were a subspecies of the South American finches he had studied earlier and had most likely been blown to sea in a storm. But as he studied distribution patterns, Darwin observed that most islands in the archipelago carried only two or three types of finches; only the larger central islands showed greater diversification. What intrigued him even more was that all the Galapagos finches differed in size and behavior. Some were heavy-billed seedeaters; others were slender billed and favored insects. Sailing through the archipelago, Darwin discovered that the finches on Hood Island were different from those on Tower Island and that both were different from those on Indefatigable Island. He began to wonder what would happen if a few finches on Hood Island were blown by high winds to another island. Darwin concluded that if the newcomers were pre-adapted to the new habitat, they would survive and multiply alongside the resident finches; if not, their number would ultimately diminish. It was one thread of what would ultimately become his famous thesis.

(Galapagos Islands, Photo by Hugoht)

Hagstrom continues:

Reviewing his notes from the voyage, Darwin was deeply perplexed. Why did the birds and tortoises on some islands of the Galapagos resemble the species found in South America while those on other islands did not? This observation was even more disturbing when Darwin learned that the finches he brought back from the Galapagos belonged to different species and were not simply different varieties of the same species, as he had previously believed. Darwin also discovered that the mockingbirds he had collected were three distinct species and the tortoises represented two species. He began referring to these troubling questions as “the species problem,” and outlined his observations in a notebook he later entitled “Notebook on the Transmutation of the Species.”

Darwin now began an intense investigation into the species variation. He devoured all the written work on the subject and exchanged voluminous correspondence with botanists, naturalists, and zookeepers–anyone who had information or opinions about species mutation. What he learned convinced him that he was on the right track with his working hypothesis that species do in fact change, whether from place to place or from time period to time period. The idea was not only radical at the time, it was blasphemous. Darwin struggled to keep his work secret.

(Photo by Maull and Polyblank (1855), via Wikimedia Commons)

It took several years–until 1838–for Darwin to put together his hypothesis. Darwin wrote in his notebook:

Being well-prepared to appreciate the struggle for existence which everywhere goes on from long-continued observation of the habits of animals and plants, it at once struck me that under these circumstances, favorable variations would tend to be preserved and unfavorable ones to be destroyed. The result of this would be the formation of new species. Here, then, I had at last got a theory–a process by which to work.

The struggle for survival was occurring not only between species, but also between individuals of the same species, Hagstrom points out. Favorable variations are preserved. After many generations, small gradual changes begin to add up to larger changes. Evolution.

Darwin delayed publishing his ideas, perhaps because he knew they would be highly controversial, notes Hagstrom. Finally, in 1859, Darwin publishedOn the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life. The book sold out on its first day. By 1872,The Origin of Species was in its sixth edition.

Hagstrom writes that in the first edition of Alfred Marshall’s famous textbook,Principles of Economics, the economist put the following on the title page:

Natura non facit saltum

Darwin himself used the same phrase–which means “nature does not make leaps”–in his book,The Origin of Species. Although Marshall never explained his thinking explicitly, it seems Marshall meant to align his work with Darwinian thinking.

Less than two decades later, Austrian-born economist Joseph Schumpeter put forth his central idea ofcreative destruction. Hagstrom quotes British economist Christopher Freeman, who–after studying Schumpeter’s life–remarked:

The central point of his whole life work is that capitalism can only be understood as an evolutionary process of continuous innovation and creative destruction.

Hagstrom explains:

Innovation, said Schumpeter, is the profitable application of new ideas, including products, production processes, supply sources, new markets, or new ways in which a company could be organized. Whereas standard economic theory believed progress was a series of small incremental steps, Schumpeter’s theory stressed innovative leaps, which in turn caused massive disruption and discontinuity–an idea captured in Schumpeter’s famous phrase “the perennial gale of creative destruction.”

But all these innovative possibilities meant nothing without the entrepreneur who becomes the visionary leader of innovation. It takes someone exceptional, said Schumpeter, to overcome the natural obstacles and resistance to innovation. Without the entrepreneur’s desire and willingness to press forward, many great ideas could never be launched.

(Image from the Department of Economics, University of Freiburg, via Wikimedia Commons)

Moreover, Schumpeter held that entrepreneurs can thrive only in certain environments. Property rights, a stable currency, and free trade are important. And credit is even more important.

In the fall of 1987, a group of physicists, biologists, and economists held a conference at the Santa Fe Institute. The economist Brian Arthur gave a presentation on “New Economics.” A central idea was to apply the concept of complex adaptive systems to the science of economics. Hagstrom records that the Santa Fe group isolated four features of the economy:

Dispersed interaction: What happens in the economy is determined by the interactions of a great number of individual agents all acting in parallel. The action of any one individual agent depends on the anticipated actions of a limited number of agents as well as on the system they cocreate.

No global controller: Although there are laws and institutions, there is no one global entity that controls the economy. Rather, the system is controlled by the competition and coordination between agents of the system.

Continual adaptation: The behavior, actions, and strategies of agents, as well as their products and services, are revised continually on the basis of accumulated experience. In other words, the system adapts. It creates new products, new markets, new institutions, and new behavior. It is an ongoing system.

Out-of-equilibrium dynamics: Unlike the equilibrium models that dominate the thinking in classical economics, the Santa Fe group believed the economy, because of constant change, operates far from equilibrium.

Hagstrom argues that different investment or trading strategies throughout history have competed against one another. Those that have most accurately predicted the future for various businesses and their associated stock prices have survived, while less profitable strategies have disappeared.

But in any given time period, once a specific strategy becomes profitable, then more money flows into it, which eventually makes it less profitable. New strategies are then invented and compete against one another. As a result, a new strategy becomes dominant and then the process repeats.

Thus, economies and markets evolve over time. There is no stable equilibrium in a market except in the short term. To go from the language of biology to the language of business, Hagstrom refers to three important books:

• Creative Destruction: Why Companies That Are Built to Last Underperform the Market–and How to Successfully Transform Them, by Richard Foster and Sarah Kaplan of McKinsey & Company
• The Innovator’s Dilemma: When New Technologies Cause Great Firms to Fail, by Clayton Christensen
• The Innovator’s Solution: Creating and Sustaining Successful Growth, by Clayton Christensen and Michael Raynor

Hagstrom sums up the lessons from biology as compared to the previous ideas from physics:

Indeed, the movement from the mechanical view of the world to the biological view of the world has been called the “second scientific revolution.” After three hundred years, the Newtonian world, the mechanized world operating in perfect equilibrium, is now the old science. The old science is about a universe of individual parts, rigid laws, and simple forces. The systems are linear: Change is proportional to the inputs. Small changes end in small results, and large changes make for large results. In the old science, the systems are predictable.

The new science is connected and entangled. In the new science, the system is nonlinear and unpredictable, with sudden and abrupt changes. Small changes can have large effects while large events may result in small changes. In nonlinear systems, the individual parts interact and exhibit feedback effects that may alter behavior. Complex adaptive systems must be studied as a whole, not in individual parts, because the behavior of the system is greater than the sum of the parts.

The old science was concerned with understanding the laws of being. The new science is concerned with the laws of becoming.

(Photo by Isabellebonaire)

Hagstrom then quotes the last passage from Darwin’sThe Origin of Species:

It is interesting to contemplate an entangled bank, clothed with many plants of many kinds, with birds singing on the bushes, with various insects flitting about, and with worms crawling through the damp earth, and to reflect that these elaborately constructed forms, so different from each other, and dependent on each other in so complex a manner, have all been produced by laws acting around us. These laws, taken in the largest sense, being Growth with Reproduction; Inheritance which is almost implied by reproduction; Variability from the indirect and direct action of the external conditions of life, and from use and disuse; a Ratio of Increase so high as to lead to a Struggle for Life, and as a consequence to Natural Selection, entailing divergence of Character and Extinction of less improved forms. Thus, from the war of nature, from famine and death, the most exalted object which we are capable of conceiving, namely, the production of higher animals, directly follows. There is grandeur in this view of life, with its several powers, having been originally breathed into a few forms or into one; and that, whilst this planet has gone cycling on according to the fixed law of gravity, from so simple a beginning endless forms most beautiful and most wonderful have been, and are being, evolved.

 

SOCIOLOGY

Because significant increases in computer power are now making vast amounts of data about human behavior available, the social sciences may at some point get enough data to figure out more precisely and more generally the laws of human behavior. But we’re not there yet.

(Auguste Comte, via Wikimedia Commons)

The nineteenth century–despite the French philosopher Auguste Comte’s efforts to establish one unified social science–ended with several distinct specialties, says Hagstrom, including economics, political science, and anthropology.

Scottish economist Adam Smith published hisWealth of Nations in 1776. Smith argued for what is now called laissez-faire capitalism, or a system free from government interference, including industry regulation and protective tariffs. Smith also held that a division of labor, with individuals specializing in various tasks, led to increased productivity. This meant more goods at lower prices for consumers, but it also meant more wealth for the owners of capital. And it implied that the owners of capital would try to limit the wages of labor. Furthermore, working conditions would likely be bad without government regulation.

Predictably, political scientists appeared on the scene to study how the government should protect the rights of workers in a democracy. Also, the property rights of owners of capital had to be protected.

Social psychologists studied how culture affects psychology, and how the collective mind affects culture. Social biologists, meanwhile, sought to apply biology to the study of society, notes Hagstrom. Recently scientists, including Edward O. Wilson, have introducedsociobiology, which involves the attempt to apply the scientific principles of biology to social development.

Hagstrom writes:

Although the idea of a unified theory of social science faded in the late nineteenth century, here at the beginning of the twenty-first century, there has been a growing interest in what we might think of as a new unified approach. Scientists have now begun to study the behavior of whole systems–not only the behavior of individuals and groups but the interactions between them and the ways in which this interaction may in turn influence subsequent behavior. Because of this reciprocal influence, our social system is constantly engaged in a socialization process the consequence of which not only alters our individual behavior but often leads to unexpected group behavior.

To explain the formation of a social group, the theory of self-organization has been developed. Ilya Prigogine, the Russian chemist, was awarded the Nobel Prize in 1977 for his thermodynamic concept of self-organization.

Paul Krugman, winner of the 2008 Nobel Prize for Economics, studied self-organization as applied to the economy. Hagstrom:

Setting aside for the moment the occasional recessions and recoveries caused by exogenous events such as oil shocks or military conflicts, Krugman believes that economic cycles are in large part caused by self-reinforcing effects. During a prosperous period, a self-reinforcing process leads to greater construction and manufacturing until the return on investment begins to decline, at which point an economic slump begins. The slump in itself becomes a self-reinforcing effect, leading to lower production; lower production, in turn, will eventually cause return on investment to increase, which starts the process all over again.

Hagstrom notes that equity and debt markets are good examples of self-organizing, self-reinforcing systems.

If self-organization is the first characteristic of complex adaptive systems, thenemergence is the second characteristic. Hagstrom says that emergence refers to the way individual units–whether cells, neurons, or consumers–combine to create something greater than the sum of the parts.

(Collective Dynamics of Complex Systems, by Dr. Hiroki Sayama, via Wikimedia Commons)

One fascinating aspect of human collectives is that, in many circumstances–like finding the shortest way through a maze–the collective solution is better when there are both smart and not-so-smart individuals in the collective. This more diverse collective outperforms a group that is composed only of smart individuals.

This implies that the stock market may more accurately aggregate information when the participants include many different types of people, such as smart and not-so-smart, long-term and short-term, and so forth, observes Hagstrom.

There are many areas where a group of people is actually smarter than the smartest individual in the group. Hagstrom mentions that Francis Galton, the English Victorian-era polymath, wrote about a contest in which 787 people guessed at the weight of a large ox. Most participants in the contest were not experts by any means, but ordinary people. The ox actually weighed 1,198 pounds. The average guess of the 787 guessers was 1,197 pounds, which was more accurate than the guesses made by the smartest and the most expert guessers.

This type of experiment can easily be repeated. For example, take a jar filled with pennies, where only you know how many pennies are in the jar. Pass the jar around in a group of people and ask each person–independently (with no discussion)–to write down their guess of how many pennies are in the jar. In a group that is large enough, you will nearly always discover that the average guess is better than any individual guess. (That’s been the result when I’ve performed this experiment in classes I’ve taught.)

In order for the collective to be that smart, the members must be diverse and the members’ guesses must be independent from one another. So the stock market is efficient when these two conditions are satisfied. But if there is a breakdown in diversity, or if individuals start copying one another too much–what Michael Mauboussin calls an information cascade–then you could have a boom, fad, fashion, or crash.

There are some situations where an individual can be impacted by the group. Solomon Asch did a famous experiment in which the subject is supposed to match lines that have the same length. It’s an easy question that every subject–if left alone–gets right. But then Asch has seven out of eight participantsdeliberately choose the wrong answer, unbeknownst to the subject of the experiment, who is the eighth participant in the same room. When this experiment was repeated many times, roughly one-third of the subjects gave the same answer as the group, even though this answer is obviously wrong. Such can be the power of a group opinion.

Hagstrom asks about how crashes can happen. Danish theoretical physicist Per Bak developed the notion ofself-organized criticality.

According to Bak, large complex systems composed of millions of interacting parts can break down not only because of a single catastrophic event but also because of a chain reaction of smaller events. To illustrate the concept of self-criticality, Bak often used the metaphor of a sand pile… Each grain of sand is interlocked in countless combinations. When the pile has reached its highest level, we can say the sand is in a state of criticality. It is just on the verge of becoming unstable.

(Computer Simulation of Bak-Tang-Weisenfeld sandpile, with 28 million grains, by Claudio Rocchini, via Wikimedia Commons)

Adding one more grain starts an avalanche. Bak and two colleagues applied this concept to the stock market. They assumed that there are two types of agents,rational agents andnoise traders. Most of the time, the market is well-balanced.

But as stock prices climb, rational agents sell and leave the market, while more noise traders following the trend join. When noise traders–trend followers–far outnumber rational agents, a bubble can form in the stock market.

 

PSYCHOLOGY

The psychologists Daniel Kahneman and Amos Tversky did research together for over two decades. Kahneman was awarded the Nobel Prize in Economics in 2002. Tversky would also have been named had he not passed away.

(Daniel Kahneman, via Wikimedia Commons)

Much of their groundbreaking research is contained inJudgment Under Uncertainty: Heuristics and Biases (1982).

Here you will find all the customary behavioral finance terms we have come to know and understand: anchoring, framing, mental accounting, overconfidence, and overreaction bias. But perhaps the most significant insight into individual behavior wasloss aversion.

Kahneman and Tversky discovered that how choices are framed–combined with loss aversion–can materially impact how people make decisions. For instance, in one of their well-known experiments, they asked people to choose between the following two options:

• (a) Save 200 lives for sure.
• (b) Have a one-third chance of saving 600 lives and a two-thirds chance of saving no one.

In this scenario, people overwhelmingly chose (a)–to save 200 lives for sure. Kahneman and Tversky next asked the same people to choose between the following two options:

• (a) Have 400 people die for sure.
• (b) Have a two-thirds chance of 600 people dying and a one-third chance of no one dying.

In this scenario, people preferred (b)–a two-thirds chance of 600 people dying, and a one-third chance of no one dying.

But the two versions of the problem are identical. The number of people saved in the first version equals the number of people who won’t die in the second version.

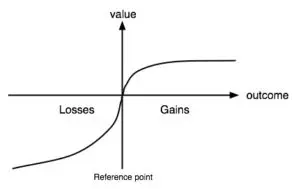
What Kahneman and Tversky had demonstrated is that people are risk averse when considering potential gains, but risk seeking when facing the possibility of a certain loss. This is the essence of prospect theory, which is captured in the following graph:

(Value function in Prospect Theory, drawing by Marc Rieger, via Wikimedia Commons)

Loss aversion refers to the fact that people weigh a potential loss about 2.5 times more than an equivalent gain. That’s why the value function in the graph is steeper for losses.

Richard Thaler and Shlomo Benartzi researched loss aversion by hypothesizing that the less frequently an investor checks the price of a stock he or she owns, the less likely the investor will be to sell the stock because of temporary downward volatility. Thaler and Benartzi invented the termmyopic loss aversion.

Hagstrom writes:

In my opinion, the single greatest psychological obstacle that prevents investors from doing well in the stock market is myopic loss aversion. In my twenty-eight years in the investment business, I have observed firsthand the difficulty investors, portfolio managers, consultants, and committee members of large institutional funds have with internalizing losses (loss aversion), made all the more painful by tabulating losses on a frequent basis (myopic loss aversion). Overcoming this emotional burden penalizes all but a very few select individuals.

Perhaps it is not surprising that the one individual who has mastered myopic loss aversion is also the world’s greatest investor–Warren Buffett…

Buffett understands that as long as the earnings of the businesses you own move higher over time, there’s no reason to worry about shorter term stock price volatility. Because Berkshire Hathaway, Buffett’s investment vehicle, holds both public stocks and wholly owned private businesses, Buffett’s long-term outlook has been reinforced. Hagstrom quotes Buffett:

I don’t need a stock price to tell me what I already know about value.

Hagstrom mentions Berkshire’s investment in The Coca-Cola Company (KO), in 1988. Berkshire invested $1 billion, which was at that time the single largest investment Berkshire had ever made. Over the ensuing decade, KO stock went up ten times, while the S&P 500 Index only went up three times. But four out of those ten years, KO stock underperformed the market. Trailing the market 40 percent of the time didn’t bother Buffett a bit.

As Hagstrom observes, Benjamin Graham–the father of value investing, and Buffett’s teacher and mentor–made a distinction between the investor focused on long-term business value and the speculator who tries to predict stock prices in the shorter term. The true investor should never be concerned with shorter term stock price volatility.

(Ben Graham, Photo by Equim43, via Wikimedia Commons)

Hagstrom quotes Graham’s The Intelligent Investor:

The investor who permits himself to be stampeded or unduly worried by unjustified market declines in his holdings is perversely transforming his basic advantage into a basic disadvantage. That man would be better off if his stocks had no market quotation at all, for he would then be spared the mental anguish caused him by another person’s mistakes of judgment.

Terence Odean, a behavioral economist, has done extensive research on the investment decisions of individuals and households. Odean discovered that:

• Many investors trade often–Odean found a 78 percent portfolio turnover ratio in his first study, which tracked 97,483 trades from ten thousand randomly selected accounts.
• Over the subsequent 4 months, one year, and two years, the stocks that investors bought consistently trailed the market, while the stocks that investors sold beat the market.

Hagstrom mentions that people use mental models as a basis for understanding reality and making decisions. But we tend to assume that each mental model we have is equally probable, rather than working to assign different probabilities to different models.

Moreover, people typically can make models for what something is–or what is true–instead of what something is not–or what is false. Also, our mental models are usually quite incomplete. And we tend to forget details of our models, especially after time passes. Finally, writes Hagstrom, people tend to construct mental models based on superstition or unwarranted belief.

Hagstrom asks the question: Why do people tend to be so gullible in general? For instance, while there’s no evidence that market forecasts have any value, many otherwise intelligent people pay attention to them and even make decisions based on them.

The answer, states Hagstrom, is that we are wired to seek and to find patterns. We have two basic mental systems, System 1 (intuition) and System 2 (reason). System 1 operates automatically. It takes mental shortcuts which often work fine, but not always. System 1 is designed to find patterns. And System 1 seeks confirming evidence for its hypotheses (patterns).

But even System 2–which humans can use to do math, logic, and statistics–uses a positive test strategy, meaning that itseeks confirming evidence for its hypotheses (patterns), rather than disconfirming evidence.

 

PHILOSOPHY

Hagstrom introduces the chapter:

A true philosopher is filled with a passion to understand, a process that never ends.

(Socrates, J. Aars Platon (1882), via Wikimedia Commons)

Metaphysics is one area of philosophy. Aesthetics, ethics, and politics are other areas. But Hagstrom focuses his discussion of philosophy onepistemology, the study of knowledge.

Having spent a few years studying the history and philosophy of science, I would say thatepistemology includes the following questions:

• What different kinds of knowledge can we have?
• What constitutes scientific knowledge?
• Is any part of our knowledge certain, or can all knowledge be improved indefinitely?
• How does scientific progress happen?

In a sense, epistemology is thinking about thinking. Epistemology is also studying the history of science in great detail, because humans have made enormous progress in generating scientific knowledge.

Studying epistemology can help us to become better, more rigorous, and more coherent thinkers, which can make us better investors.

Hagstrom makes it clear in the Preface that his book is necessarily abbreviated, otherwise it would have been a thousand pages long. That said, had he been aware of Willard Van Orman Quine’s epistemology, Hagstrom likely would have mentioned it.

Here is a passage from Quine’sFrom A Logical Point of View:

The totality of our so-called knowledge or beliefs, from the most casual matters of geography and history to the profoundest laws of atomic physics or even of pure mathematics and logic, is a man-made fabric which impinges on experience only along the edges. Or, to change the figure, total science is like a field of force whose boundary conditions are experience. A conflict with experience at the periphery occasions readjustments in the interior of the field. Truth values have to be redistributed over some of our statements. Re-evaluation of some statements entails re-evaluation of others, because of their logical interconnections–the logical laws being in turn simply certain further statements of the system, certain further elements of the field. Having re-evaluated one statement we must re-evaluate some others, which may be statements logically connected with the first or may be the statements of logical connections themselves. But the total field is so underdetermined by its boundary conditions, experience, that there is much latitude of choice as to what statements to re-evaluate in the light of any single contrary experience. No particular experiences are linked with any particular statements in the interior of the field, except indirectly through considerations of equilibrium affecting the field as a whole.

If this view is right, it is misleading to speak of the empirical content of an individual statement–especially if it is a statement at all remote from the experiential periphery of the field. Furthermore it becomes folly to seek a boundary between synthetic statements, which hold contingently on experience, and analytic statements, which hold come what may. Any statement can be held true come what may, if we make drastic enough adjustments elsewhere in the system. Even a statement very close to the periphery can be held true in the face of recalcitrant experience by pleading hallucination or by amending certain statements of the kind called logical laws. Conversely, by the same token, no statement is immune to revision. Revision even of the logical law of the excluded middle has been proposed as a means of simplifying quantum mechanics…

(Image by Dmytro Tolokonov)

Quine continues:

For vividness I have been speaking in terms of varying distances from a sensory periphery. Let me now try to clarify this notion without metaphor. Certain statements, thoughabout physical objects and not sense experience, seem peculiarly germane to sense experience–and in a selective way: some statements to some experiences, others to others. Such statements, especially germane to particular experiences, I picture as near the periphery. But in this relation of “germaneness” I envisage nothing more than a loose association reflecting the relative likelihood, in practice, of our choosing one statement rather than another for revision in the event of recalcitrant experience. For example, we can imagine recalcitrant experiences to which we would surely be inclined to accomodate our system by re-evaluating just the statement that there are brick houses on Elm Street, together with related statements on the same topic. We can imagine other recalcitrant experiences to which we would be inclined to accomodate our system by re-evaluating just the statement that there are no centaurs, along with kindred statements. A recalcitrant experience can, I have urged, be accomodated by any of various alternative re-evaluations in various alternative quarters of the total system; but, in the cases which we are now imagining, our natural tendency to disturb the total system as little as possible would lead us to focus our revisions upon these specific statements concerning brick houses or centaurs. These statements are felt, therefore, to have a sharper empirical reference than highly theoretical statements of physics or logic or ontology. The latter statements may be thought of as relatively centrally located within the total network, meaning merely that little preferential connection with any particular sense data obtrudes itself.

As an empiricist, I continue to think of the conceptual scheme of science as a tool, ultimately, for predicting future experience in the light of past experience. Physical objects are conceptually imported into the situation as convenient intermediaries–not by definition in terms of experience, but simply as irreducible posits comparable, epistemologically, to the gods of Homer. For my part I do, qua lay physicist, believe in physical objects and not in Homer’s gods; and I consider it a scientific error to believe otherwise. But in point of epistemological footing the physical objects and the gods differ only in degree and not in kind. Both sorts of entities enter our conception only as cultural posits. The myth of physical objects is epistemologically superior to most in that it has proved more efficacious than other myths as a device for working a manageable structure into the flux of experience.

…

Physical objects, small and large, are not the only posits. Forces are another example; and indeed we are told nowadays that the boundary between energy and matter is obsolete. Moreover, the abstract entities which are the substance of mathematics–ultimately classes and classes of classes and so on up–are another posit in the same spirit. Epistemologically these are posits on the same footing with physical objects and gods, neither better nor worse except for differences in the degree to which they expedite our dealings with sense experiences.

Historically, philosophers distinguished between “analytic” statements, which were thought to be true by definition, and “synthetic” statements, which were thought to be true on the basis of certain empirical data or experiences. One of Quine’s chief points is that this distinction doesn’t hold.

Mathematics, logic, scientific theories, scientific laws, working hypotheses, ordinary language, and much else including simple observations, are all a part of science.The goal of science–which extends common sense–is to predict various future experiences–including experiments–on the basis of past experiences.

When predictions–including experiments–don’t turn out as expected, then any part of the totality of science is revisable. Often it makes sense to revise specific hypotheses, or specific statements that are close to experience. But sometimes highly theoretical statements or ideas–including the laws of mathematics, the laws of logic, and the most well-established scientific laws–are revised in order to make the overall system of science work better, i.e., predict phenomena (future experiences) better, with more generality or with more exactitude.

The chief way scientists have made–and continue to make–progress is by testing predictions that are implied by existing scientific theory or law, or that are implied by new hypotheses under consideration.

(Top quark and anti top quark pair decaying into jets, Collider Detector at Fermilab, via Wikimedia Commons)

Because of recent advances in computing power and because of the explosion of shared knowledge, ideas, and experiments on the internet, scientific progress is probably happening much faster than ever before. It’s a truly exciting time for all curious people and scientists. And once artificial intelligence passes thesingularity threshold, scientific progress is likely to skyrocket, even beyond what we can imagine.

 

LITERATURE

Critical reading is a crucial part of becoming a better thinker.

(Photo by VijayGES2, via Wikimedia Commons)

One excellent book about how to read analytically isHow to Read a Book, by Mortimer J. Adler. The goal of analytical reading is to improve your understanding–as opposed to only gaining information. To this end, Adler suggests active readers keep the following four questions in mind:

• What is the book about as a whole?
• What is being said in detail?
• Is the book true, in whole or part?
• What of it?

Before deciding to read a book in detail, it can be helpful to read the preface, table of contents, index, and bibliography. Also, read a few paragraphs at random. These steps will help you to get a sense of what the book is about as a whole. Next, you can skim the book to learn more about what is being said in detail, and whether it’s worth reading the entire book carefully.

Then, if you decide to read the entire book carefully, you should approach it like you would approach assigned reading for a university class. Figure out the main points and arguments. Take notes if that helps you learn. The goal is to understand the author’s chief arguments, and whether–or to what extent–those arguments are true.

The final step iscomparative reading, says Hagstrom. Adler considers this the hardest step. Here the goal is to learn about a specific subject. You want to determine which books on the subject are worth reading, and then compare and contrast these books.

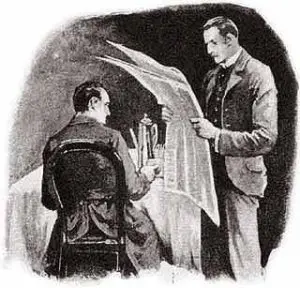
Hagstrom points out that the three greatest detectives in fiction are Auguste Dupin, Sherlock Holmes, and Father Brown. We can learn much from studying the stories involving these sleuths.

Auguste Dupin was created by Edgar Allan Poe. Hagstrom remarks that we can learn the following from Dupin’s methods:

• Develop a skeptic’s mindset; don’t automatically accept conventional wisdom.
• Conduct a thorough investigation.

Sherlock Holmes was created by Sir Arthur Conan Doyle.

(Illustration by Sidney Paget (1891), via Wikimedia Commons)

From Holmes, we can learn the following, says Hagstrom:

• Begin an investigation with an objective and unemotional viewpoint.
• Pay attention to the tiniest details.
• Remain open-minded to new, even contrary, information.
• Apply a process of logical reasoning to all you learn.

Father Brown was created by G. K. Chesterton. From Father Brown, we can learn:

• Become a student of psychology.
• Have faith in your intuition.
• Seek alternative explanations and redescriptions.

Hagstrom ends the chapter by quoting Charlie Munger:

I believe in… mastering the best that other people have figured out [rather than] sitting down and trying to dream it up yourself… You won’t find it that hard if you go at it Darwinlike, step by step with curious persistence. You’ll be amazed at how good you can get… It’s a huge mistake not to absorb elementary worldly wisdom… Your life will be enriched–not only financially but in a host of other ways–if you do.

 

MATHEMATICS

Hagstrom quotes Warren Buffett:

…the formula for valuing ALL assets that are purchased for financial gain has been unchanged since it was first laid out by a very smart man in about 600 B.C.E. The oracle was Aesop and his enduring, though somewhat incomplete, insight was “a bird in the hand is worth two in the bush.” To flesh out this principle, you must answer only three questions. How certain are you that there are indeed birds in the bush? When will they emerge and how many will there be? What is the risk-free interest rate? If you can answer these three questions, you will know the maximum value of the bush–and the maximum number of birds you now possess that should be offered for it. And, of course, don’t literally think birds. Think dollars.

Hagstrom explains that it’s the same formula whether you’re evaluating stocks, bonds, manufacturing plants, farms, oil royalties, or lottery tickets. As long as you have the numbers needed for the calculation, the attractiveness of all investment opportunities can be evaluated and compared.

So to value any business, you have to estimate the future cash flows of the business, and then discount those cash flows back to the present. This is the DCF–discounted cash flows–method for determining the value of a business.

Although Aesop gave the general idea, John Burr Williams, inThe Theory of Investment Value (1938), was the first to explain the DCF approach explicitly. Williams had studied mathematics and chemistry as an undergraduate at Harvard University. After working as a securities analyst, Williams returned to Harvard to get a PhD in economics.The Theory of Investment Value was Williams’ dissertation.

Hagstrom writes that in 1654, the Chevalier de Méré, a French nobleman who liked to gamble, asked the mathematician Blaise Pascal the following question: “How do you divide the stakes of an unfinished game of chance when one of the players is ahead?”

(Photo by Rossapicci, via Wikimedia Commons)

Pascal was a child prodigy and a brilliant mathematician. To help answer de Méré’s question, Pascal turned to Pierre de Fermat, a lawyer who was also a brilliant mathematician. Hagstrom reports that Pascal and Fermat exchanged a series of letters which are the foundation of what is now calledprobability theory.

There are two broad categories of probabilities:

• frequency probability
• subjective probability

A frequency probability typically refers to a system that can generate a great deal of statistical data over time. Examples include coin flips, roulette wheels, cards, and dice, notes Hagstrom. For instance, if you flip a coin 1,000 times, you expect to get heads about 50 percent of the time. If you roll one 6-sided dice 1,000 times, you expect to get each number about 16.67 percent of the time.

If you don’t have a sufficient frequency of events, plus a long time period to analyze results, then you must rely on a subjective probability. A subjective probability, says Hagstrom, is often a reasonable assessment made by a knowledgeable person. It’s a best guess based a logical analysis of the given data.

When using a subjective probability, obviously you want to make sure you have all the available data that could be relevant. And clearly you have to use logic correctly.

But the key to using a subjective probability is to update your beliefs as you gain new data. The proper way to update your beliefs is by using Bayes’ Rule.

(Thomas Bayes, via Wikimedia Commons)

Bayes’ Rule

Eliezer Yudkowsky of the Machine Intelligence Research Institute provides an excellent intuitive explanation of Bayes’ Rule:http://www.yudkowsky.net/rational/bayes

Yudkowsky begins by discussing a situation that doctors often encounter:

1% of women at age forty who participate in routine screening have breast cancer. 80% of women with breast cancer will get positive mammographies. 9.6% of women without breast cancer will also get positive mammographies. A woman in this age group had a positive mammography in a routine screening. What is the probability that she actually has breast cancer?

Most doctors estimate the probability between 70% and 80%, which is wildly incorrect.

In order to arrive at the correct answer, Yudkowsky asks us to think of the question as follows. We know that 1% of women at age forty who participate in routine screening have breast cancer. So consider 10,000 women who participate in routine screening:

• Group 1: 100 womenwithbreast cancer.
• Group 2: 9,900 womenwithoutbreast cancer.

After the mammography, the women can be divided into four groups:

• Group A: 80 womenwith breast cancer, and apositive mammography.
• Group B: 20 womenwith breast cancer, and anegative mammography.
• Group C: 950 womenwithout breast cancer, and apositivemammography.
• Group D: 8,950 womenwithoutbreast cancer, and anegative mammography.

So the question again: If a woman out of this group of 10,000 women has a positive mammography, what is the probability that she actually has breast cancer?

The total number of women who hadpositive mammographies is 80 + 950 = 1,030. Of that total, 80 women hadpositive mammographies AND have breast cancer. In looking at the total number of positive mammographies (1,030), we know that 80 of them actually have breast cancer.

So if a woman out of the 10,000 has a positive mammography, the chances that she actually has breast cancer = 80/1030 or 0.07767 or 7.8%.

That’s the intuitive explanation. Now let’s look atBayes’Rule:

P(A|B) = [P(B|A)P(A)] /P(B)

Let’s apply Bayes’ Rule to the same question above:

1% of women at age forty who participate in routine screening have breast cancer. 80% of women with breast cancer will get positive mammographies. 9.6% of women without breast cancer will also get positive mammographies. A woman in this age group had a positive mammography in a routine screening. What is the probability that she actually has breast cancer?

P(A|B) = the probability that the woman has breast cancer (A), given a positive mammography (B)

Here is what we know:

P(B|A) = 80% – the probability of a positive mammography (B), given that the woman has breast cancer (A)

P(A) = 1% – the probability that a woman out of the 10,000 screened actually has breast cancer

P(B) = (80+950) / 10,000 = 10.3% – the probability that a woman out of the 10,000 screened has a positive mammography

Bayes’ Rule again:

P(A|B) = [P(B|A)P(A)] /P(B)

P(A|B) = [0.80*0.01] / 0.103 = 0.008 / 0.103 = 0.07767 or 7.8%

Derivation of Bayes’ Rule:

Bayesians consider conditional probabilities as more basic than joint probabilities. You can define P(A|B) without reference to the joint probability P(A,B). To see this, first start with the conditional probability formula:

P(A|B) P(B) = P(A,B)

but by symmetry youget:

P(B|A) P(A) = P(A,B)

It follows that:

P(A|B) = [P(B|A)P(A)] /P(B)

which isBayes’ Rule.

In conclusion, Hagstrom makes the important observation that there is much we still don’t know about nature and about ourselves. (The question mark below is by Khaydock, via Wikimedia Commons.)

Nothing is absolutely certain.

One clear lesson from history–whether the history of investing, the history of science, or some other area–is that very often people who are “absolutely certain” about something turn out to be wrong.

Economist and Nobel laureate Kenneth Arrow:

• Our knowledge of the way things work, in society or in nature, comes trailing clouds of vagueness. Vast ills have followed a belief in certainty.

Investor and author Peter Bernstein:

The recognition of risk management as a practical art rests on a simple cliché with the most profound consequences: when our world was created, nobody remembered to include certainty. We are never certain; we are always ignorant to some degree. Much of the information we have is either incorrect or incomplete.

 

DECISION MAKING

Take a few minutes and try answering these three problems:

• A bat and a ball cost $1.10. The bat costs one dollar more than the ball. How much does the ball cost?
• If it takes 5 machines 5 minutes to make 5 widgets, how long would it take 100 machines to make 100 widgets?
• In a lake, there is a patch of lily pads. Every day the patch doubles in size. If it takes 48 days for the patch to cover the entire lake, how long will it take for the patch to cover half the lake?

Roughly 75 percent of the Princeton and Harvard students got at least one problem wrong. These questions form the Cognitive Reflection Test, invented by Shane Frederick, an assistant professor of management science at MIT.

Recall that System 1 (intuition) is quick, associative, and operates automatically all the time. System 2 (reason) is slow and effortful–it requires conscious activation and sustained focus–and it can learn to solve problems involving math, statistics, or logic.

To understand the mental mistake that many people–including smart people–make, let’s consider the first of the three questions:

• A bat and a ball cost $1.10. The bat costs one dollar more than the ball. How much does the ball cost?

After we read the question, our System 1 (intuition) immediately suggests to us that the bat costs $1.00 and the ball costs 10 cents. But if we slow down just a moment and engage System 2, we realize that if the bat costs $1.00 and the ball costs 10 cents, then the bat costs only 90 cents more than the ball. This violates the condition stated in the problem that the bat costs one dollar more than the ball. If we think a bit more, we see that the bat must cost $1.05 and the ball must cost 5 cents.

System 1 takes mental shortcuts, which often work fine. But when we encounter a problem that requires math, statistics, or logic, we have to train ourselves to slow down and to think through the problem. If we don’t slow down in these situations, we’ll often jump to the wrong conclusion.

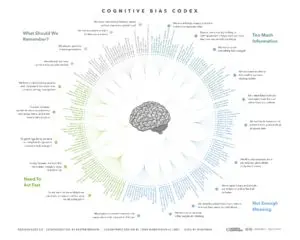
(Cognitive Bias Codex, by John Manoogian III, via Wikimedia Commons. For a closer look, try this link:https://upload.wikimedia.org/wikipedia/commons/1/18/Cognitive_Bias_Codex_-_180%2B_biases%2C_designed_by_John_Manoogian_III_%28jm3%29.jpg)

It’s possible to train your intuition under certain conditions, according to Daniel Kahneman. Hagstrom:

Kahneman believes there are indeed cases where intuitive skill reveals the answer, but that such cases are dependent on two conditions. First, “the environment must be sufficiently regular to be predictable” second, there must be an “opportunity to learn these regularities through prolonged practice.” For familiar examples, think about the games of chess, bridge, and poker. They all occur in regular environments, and prolonged practice at them helps people develop intuitive skill. Kahneman also accepts the idea that army officers, firefighters, physicians, and nurses can develop skilled intuition largely because they all have had extensive experience in situations that, while obviously dramatic, have been repeated many times over.

Kahneman concludes that intuitive skill exists mostly in people who operate in simple, predictable environments and that people in more complex environments are much less likely to develop this skill. Kahneman, who has spent much of his career studying clinicians, stock pickers, and economists, notes that evidence of intuitive skill is largely absent in this group. Put differently, intuition appears to work well in linear systems where cause and effect is easy to identify. But in nonlinear systems, including stock markets and economies, System 1 thinking, the intuitive side of our brain, is much less effectual.

Experts in fields such as investing, economics, and politics have, in general, not demonstrated the ability to make accurate forecasts or predictions with any reliable consistency.

Philip Tetlock, professor of psychology at the University of Pennsylvania, tracked 284 experts over fifteen years (1988-2003) as they made 27,450 forecasts. The results are no better than “dart-throwing chimpanzees,” as Tetlock describes inExpert Political Judgment: How Good Is It? How Can We Know? (Princeton University Press, 2005).

Hagstrom explains:

It appears experts are penalized, like the rest of us, by thinking deficiencies. Specifically, experts suffer from overconfidence, hindsight bias, belief system defenses, and lack of Bayesian process.

Hagstrom then refers to an essay by Sir Isaiah Berlin, “The Hedgehog and the Fox: An Essay on Tolstoy’s View of History.” Hedgehogs view the world using one large idea, while Foxes are skeptical of grand theories and instead consider a variety of information and experiences before making decisions.

(Photo of Hedgehog, by Nevit Dilmen, via Wikimedia Commons)

Tetlock found that Foxes, on the whole, were much more accurate than Hedgehogs. Hagstrom:

Why are hedgehogs penalized? First, because they have a tendency to fall in love with pet theories, which gives them too much confidence in forecasting events. More troubling, hedgehogs were too slow to change their viewpoint in response to discomfirming evidence. In his study, Tetlock said Foxes moved 59 percent of the prescribed amount toward alternate hypotheses, while Hedgehogs moved only 19 percent. In other words, Foxes were much better at updating their Bayesian inferences than Hedgehogs.

Unlike Hedgehogs, Foxes appreciate the limits of their knowledge. They have better calibration and discrimination scores than Hedgehogs. (Calibration, which can be thought of as intellectual humility, measures how much your subjective probabilities correspond to objective probabilities. Discrimination, sometimes called justified decisiveness, measures whether you assign higher probabilities to things that occur than to things that do not.)

(Photo of Fox, by Alan D. Wilson, via Wikimedia Commons)

Hagstrom comments thatFoxes have three distinct cognitive advantages, according to Tetlock:

• They begin with “reasonable starter” probability estimates. They have better “inertial-guidance” systems that keep their initial guesses closer to short-term base rates.
• They are willing to acknowledge their mistakes and update their views in response to new information. They have a healthy Bayesian process.
• They can see the pull of contradictory forces, and, most importantly, they can appreciate relevant analogies.

Hagstrom concludes that the Fox “is the perfect mascot for The College of Liberal Arts Investing.”

Many people with high IQ have difficulty making rational decisions. Keith Stanovich, professor of applied psychology at the University of Toronto, invented the term dysrationalia to refer to the inability to think and behave rationally despite high intelligence, remarks Hagstrom. There are two principal causes of dysrationalia:

• a processing problem
• a content problem

Stanovich explains that people are lazy thinkers in general, preferring to think in ways that require less effort, even if those methods are less accurate. As we’ve seen, System 1 operates automatically, with little or no effort. Its conclusions are often correct. But when the situation calls for careful reasoning, the shortcuts of System 1 don’t work.

Lack of adequate content is amindware gap, says Hagstrom.Mindware refers to rules, strategies, procedures, and knowledge that people possess to help solve problems. Harvard cognitive scientist David Perkins coined the termmindware. Hagstrom quotes Perkins:

What is missing is the metacurriculum–the ‘higher order’ curriculum that deals with good patterns of thinking in general and across subject matters.

Perkins’ proposed solution is amindware booster shot, which means teaching new concepts and ideas in “a deep and far-reaching way,” connected with several disciplines.

Of course, Hagstrom’s book,Investing: The Last Liberal Art, is a great example of amindware booster shot.

 

Hagstrom concludes by stressing the vital importance of lifelong, continuous learning. Buffett and Munger have always highlighted this as a key to their success.

(Statue of Ben Franklin in front of College Hall, Philadelphia, Pennsylvania, Photo by Matthew Marcucci, via Wikimedia Commons)

Hagstrom:

Although the greatest number of ants in a colony will follow the most intense pheromone trail to a food source, there are always some ants that are randomly seeking the next food source. When Native Americans were sent out to hunt, most of those in the party would return to the proven hunting grounds. However, a few hunters, directed by a medicine man rolling spirit bones, were sent in different directions to find new herds. The same was true of Norwegian fishermen. Each day most of the ships in the fleet returned to the same spot where the previous day’s catch had yielded the greatest bounty, but a few vessels were also sent in random directions to locate the next school of fish. As investors, we too must strike a balance between exploiting what is most obvious while allocating some mental energy to exploring new possibilities.

Hagstrom adds:

The process is similar to genetic crossover that occurs in biological evolution. Indeed, biologists agree that genetic crossover is chiefly responsible for evolution. Similarly, the constant recombination of our existing mental building blocks will, over time, be responsible for the greatest amount of investment progress. However, there are occasions when a new and rare discovery opens up new opportunities for investors. In much the same way that mutation can accelerate the evolutionary process, so too can new ideas speed us along in our understanding of how markets work. If you are able to discover a new building block, you have the potential to add another level to your model of understanding.

 

BOOLE MICROCAP FUND

An equal weighted group of micro caps generally far outperforms an equal weighted (or cap-weighted) group of larger stocks over time. See the historical chart here: https://boolefund.com/best-performers-microcap-stocks/

This outperformance increases significantly by focusing on cheap micro caps. Performance can be further boosted by isolating cheap microcap companies that show improving fundamentals. We rank microcap stocks based on these and similar criteria.

There are roughly 10-20 positions in the portfolio. The size of each position is determined by its rank. Typically the largest position is 15-20% (at cost), while the average position is 8-10% (at cost). Positions are held for 3 to 5 years unless a stock approachesintrinsic value sooner or an error has been discovered.

The mission of the Boole Fund is to outperform the S&P 500 Index by at least 5% per year (net of fees) over 5-year periods. We also aim to outpace the Russell Microcap Index by at least 2% per year (net). The Boole Fund has low fees.

 

If you are interested in finding out more, please e-mail me or leave a comment.

My e-mail: jb@boolefund.com

 

 

 

Disclosures: Past performance is not a guarantee or a reliable indicator of future results. All investments contain risk and may lose value. This material is distributed for informational purposes only. Forecasts, estimates, and certain information contained herein should not be considered as investment advice or a recommendation of any particular security, strategy or investment product. Information contained herein has been obtained from sources believed to be reliable, but not guaranteed.No part of this article may be reproduced in any form, or referred to in any other publication, without express written permission of Boole Capital, LLC.